11. | M.I. of a thin uniform circular ring about the tangent to the plane of the ring is (CPMT 92) (a) 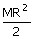 (b) MR 2(c) 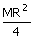 (d) 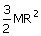
Answer: (d) |
12. | A thin uniform ring of mass M and radius R passing through its centre and perpendicular to its plane. Then its M.I. is, (CPMT 82) (a) 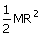 (b) MR 2(c) 2MR 2 (d) 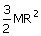 Answer: (b) |
13. | Ratio of rotational K.E. to rolling K.E. of a solid sphere is [MH-CET 2002] (a) 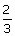 (b) 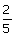 (c) 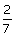 (d) 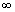 Answer: (c) |
14. | A body of M.I. of 5 kg m2, rotating with an angular velocity of 6 rad/s, has the same kinetic energy as a mass of 20 kg, moving with a velocity of (a) 3 m/s (b) 2 m/s (c) 4 m/s (d) 5 m/s Answer: (a) |
15. | A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocityw. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed of the composite disc will be (IIT 86) (a) 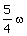 (b) 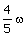 (c) 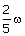 (d) 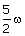 Answer: (b) |
16. | A wheel having a moment of inertia of 2 kg m2 about its vertical axis, is rotating at the rate of 60 r.p.m. about this axis. What is the retarding torque required to stop its rotation one minute? (a) 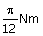 (b) 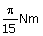 (c) 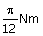 (d) 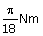 Answer: (b) |
17. | Two bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio of (a) 1:2 (b) 2:1 (c) 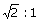 (d) 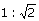 Answer: (d) |
18. | A particle of mass m is moving with a constant velocity along a line parallel to the +ve direction of the X-axis. The magnitude of its angular momentum w.r.t the origin (a) Is zero (b) Goes on increasing as x is increased (c) Goes on decreasing as x is increased (d) Remains constant for all positions of the particle Answer: (d) |
19. | Torqueses of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. Both of them are free to rotate about their axis of symmetry. If ac and as are the angular accelerations of the cylinder and the sphere respectively, then the ratio 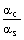 will be Answer: (b) |
20. | A dancer on ice spins faster when she folds here arms. This is due to (CPMT. PMT MP 86) (a) Increases in energy and increase in angular momentum (b) Decrease in friction at the skates (c) Constant angular momentum and increase in kinetic energy (d) Increase in energy an decreases in angular momentum Answer: (c) |
21. | The moment of inertia of a loop of radius R and mass M about any tangent line will be (CPMT 92) Answer: (a) |
22. | A mass is revolving in a circle which is in the plane of the paper. The direction of angular acceleration is (CPMT 83) (a) Upward to the radius (b) Towards the radius (c) Tangential (d) At right angle to angular velocity Answer: (c) |
23. | Angular momentum is (CBSE 93) (a) A scalar (b) A polar vector (c) A scalar as well as vector (d) An axial vector Answer: (d) |
24. | Which is the wrong relation from the following? (MH-CET 99) (a) t = I a (b) F = ma (c) L = I w (d) I = t a Answer: (d) |
25. | Two circular discs A and B have equal masses and uniform thickness but have densities r1 and r2 such that r1 > r2. their moment of inertia is (MHT-CET-2000) (a) I1 > I2 (b) I1 >> I2 (c) I1 < I2 (d) I1 = I2 Answer: (c) |